需求
由用户输入一系列对称的点,对称轴未知。
需求分析
对称的点包括对称点和对称轴上的点。可以先要求用户(图形化)输入成对的对称点,程序计算出对称轴后,再由用户输入轴上的点,并将点修正到轴上。
实际上计算对称轴的过程是对对称点中垂线求平均。但是要注意的是,输入点的误差是一个恒定值,以真实点为中心,越远概率越小。因此两对称点的连线的误差跟连线长度负相关。
而对用户输入的点的修正,其实是计算点到直线的垂足坐标,是一个简单的的解析几何问题。
解决方案
第一步,通过用户输入的对称点解出对称轴
算法思路
计算出对称轴的基本思路分为两步,先通过输入的对称点的连线计算对称轴的斜率;然后计算在这个斜率下使得对称点中点距该线距离最小时的截距。
对称轴斜率的计算
斜率的计算需要先计算对称点的方向向量,再计算与该方向向量垂直的向量,即为对称轴的方向向量。求解如下:
$$
\forall \ \textrm{symmtrical points} \ A(x_1,y_1), B(x_1',y_1') \
$$
$$
\exists \ \textrm{middle point} \ M(x_0,y_0)=(\frac{x_1+x_1'}{2} , \frac{y_1+y_1'}{2})
$$
$$
\forall \ \overrightarrow{a} = (x', y') = (x_1' - x_1, y_1' - y_1),\ \overrightarrow{n} = (x, y)
$$
$$
\exists \ \textrm{distance}\ D = |\overrightarrow{a}| = \sqrt{(x_1' - x_1)^2 +(y_1' - y_1)^2}
$$
$$
\because \overrightarrow{a} \perp \overrightarrow{n}
$$
$$
\therefore \overrightarrow{a} \cdot \overrightarrow{n} = xx'+yy' = 0
$$
$$
\Rightarrow y = -\frac{xx'}{y'}
$$
为了计算方便,确保方向向量为正值,令\(x = 1\)
$$
\therefore y = - \frac{x'}{y'}
$$
$$
e.g. \overrightarrow{n} = (1, - \frac{x'}{y'}) = (1, - \frac{x_1' - x_1}{y_1' - y_1} )
$$
正常情况下,这时候斜率就应该是\(-x'/y'\)。然而本例中有多个对称点,需要用连线长度做权,对倾角求加权平均。注意,是倾角而非斜率做加权平均,所以我们要转换为倾角:
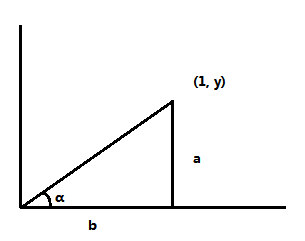
$$
tan \alpha = \frac{a}{b}
$$
$$
\because a = y, b = 1
\therefore tan \alpha = y
$$
$$
\therefore \alpha = arctan y
$$
值得注意的是,当\(y_1' = y_1\) 即 \(y' = 0\) 时,会出现0做除数的情况。
因为 \(arctanx\)的定义域为\((-∞, +∞)\), 值域为\((-π/2, π/2)\):
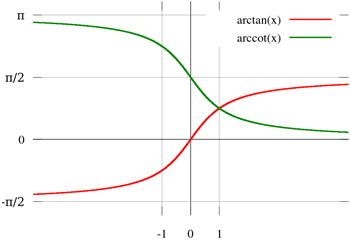
而倾角的有效范围是\([0,π)\),所以需要一次转换。
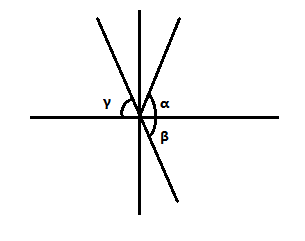
因为\(∠β\)与\(∠γ\)角度上相等,所以\(∠β\)要转换成线的倾角,即\(∠γ\)的补角,因\(∠β\)为负数,只需要对计算出的倾角为负的值加上\(π\)即可。
(之所以要将倾角归到\([0,π)\),是因为要求平均角度。如果直接求\(∠α\)和\(∠β\)平均角度的话,会得到\(0°\)。而我们想得到的是\(90°\),所以必须要用\(∠γ\)的补角取平均。)
计算对称轴的斜率\(k\):
$$
\overline{\alpha} = \frac{\sum D_i \alpha_i }{\sum D_i}
$$
$$
k = tan\overline{\alpha}
$$
对称轴截距的计算
因为对于恒定的斜率,点到直线的距离和点在y方向上到直线的距离是成正比的,即\(a = k·b\)
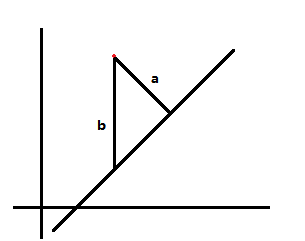
因此要计算恒定斜率下,与若干点距离(a)最短的直线。和求若干点在y方向距离(b)最短的直线是等价的。
只需要假定截距为0,计算各个点的y值与直线上相应y值之差,再求平均值即为截距。
$$
\textrm{line }L_0 : y = k x
$$
$$
\textrm{middle point }M_i = (x_m_i, y_m_i)
$$
$$
d = \frac{\sum d_i D_i}{\sum D_i} = \frac{\sum (y_m_i - k x_m_i) D_i}{\sum D_i}
$$
$$
\therefore \textrm{symmetry axis } L : y = k x + d
$$
代码
很多计算是由numpy的矩阵计算完成的,因此代码比较简单
代码中self.rawData['symmMark']是用户输入的对称点的数据,数据结构为一个一维数组, x 坐标 y 坐标依次排列。
如\(A1(x1, y1) A'1(x'1, y'1)\) 是第一对对称点,\(A2(x2, y2) A'2(x'2, y'2)\)是第二对对称点。其保存在self.rawData['symmMark']中的形式为: [x1, y1, x'1, y'1, x2, y2, x'2, y'2]
import numpy as np
# 省略其它代码...
def calcAxis(self):
smlen = len(self.rawData['symmMark'])
if smlen < 4:
return
sms = self.rawData['symmMark']
# 中点坐标
mxs = np.array([(sms[i] + sms[i + 2])/2.0 for i in xrange(0, smlen, 4)], dtype = 'float')
mys = np.array([(sms[i] + sms[i + 2])/2.0 for i in xrange(1, smlen, 4)], dtype = 'float')
# 对称点连线向量
axs = np.array([sms[i + 2] - sms[i] for i in xrange(0, smlen, 4)], dtype = 'float')
ays = np.array([sms[i + 2] - sms[i] for i in xrange(1, smlen, 4)], dtype = 'float')
# 对称点连线长度
ds = np.sqrt(np.square(axs) + np.square(ays))
# 计算与连线垂直向量的角度
angs = np.choose(np.not_equal(ays, 0), (np.PINF, - axs / ays))
# 注意:若 y0 = 0 则使结果为正无穷,这样在numpy.arctan中可以得到一个-2/π
angs = np.arctan(angs) # 同时y值和余弦值相等 计算角度
angs = np.choose(angs < 0, (angs, angs + np.pi)) # 保证角度结果在 0 ~ π 范围内
# 用连线长度加权计算平均倾角
mainang = np.sum(angs * ds) / np.sum (ds)
# 计算斜率 也就是直线方程中的a
a = np.tan(mainang)
# 假定截距为0 计算在Y轴方向上 中点到直线的距离
dys = mys - mxs * a
# 用连线长度加权计算平均截距
b = np.sum(dys * ds) / np.sum (ds)
self.axis = [a, b]
pass
第二步,将接下来用户输入的点投射到对称轴上
设输入点为\(C(x1, y1)\), 对称轴为 \(y = a x + b\)
设垂直于对称轴,通过点C的直线斜率为k 则有 \(k · a = -1\)
于是直线方程为: \(y - y1 = - 1/a (x - x1)\)
化为斜截式: \(y = -1/a x + x1/a + y1\)
与对称轴方程联立解得交点x坐标为
$$
\frac{x_1 + y_1 -b}{a + \frac{1}{a}}
$$
带入对称轴方程可得y坐标
代码
def addAxisMark(self, x, y):
if self.axis[0] == 0:
resx = x
else:
resx = (x / self.axis[0] + y - self.axis[1]) / (self.axis[0] + 1 / self.axis[0])
resy = resx * self.axis[0] + self.axis[1]
self.rawData['axisMark'].append(resx)
self.rawData['axisMark'].append(resy)
return (resx, resy)
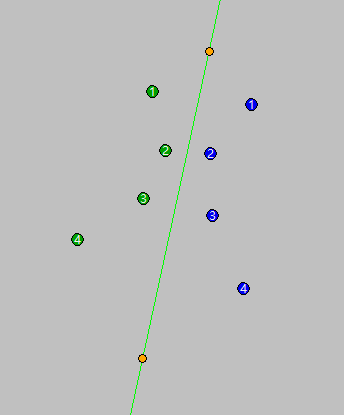
结果展示
标记数字相同的圆圈为鼠标点击输入一对对称点,绿色的线为计算出的对称轴,橙色的点为鼠标点击后修正到轴上之后的点。


There are comments.